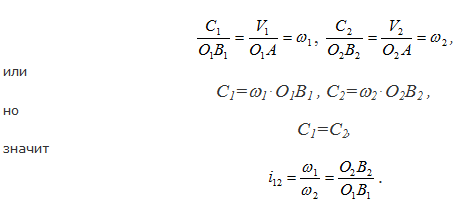
Энциклопедия по машиностроению XXL
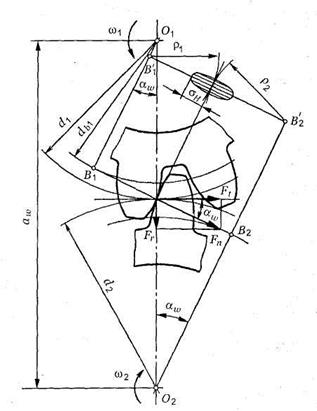
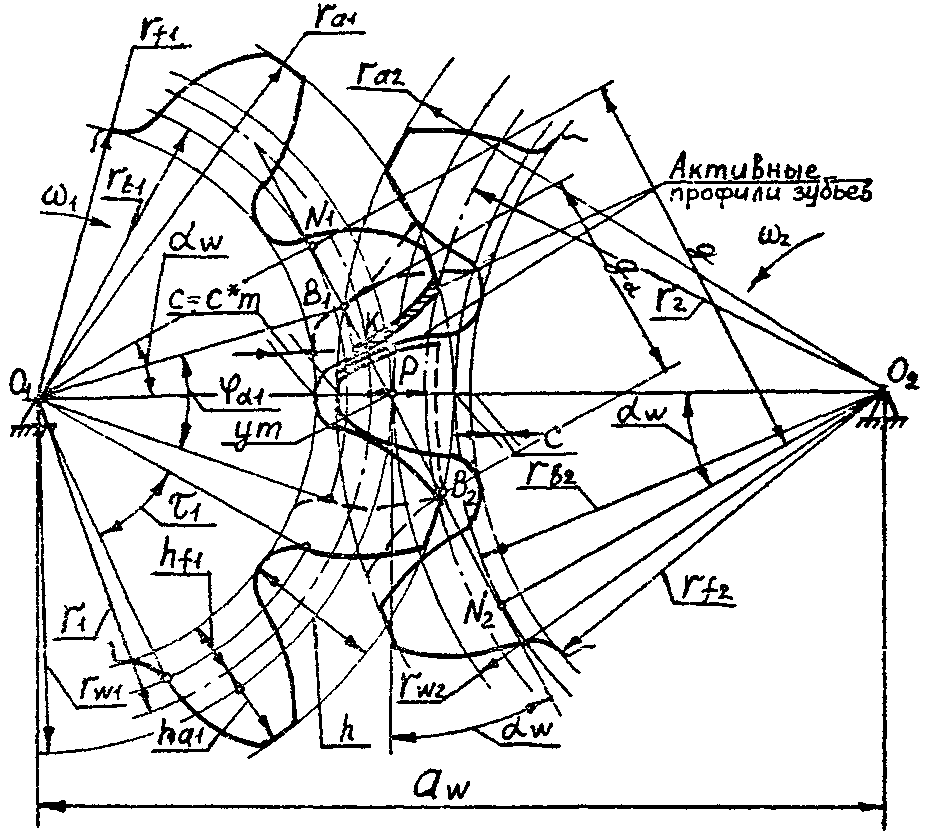
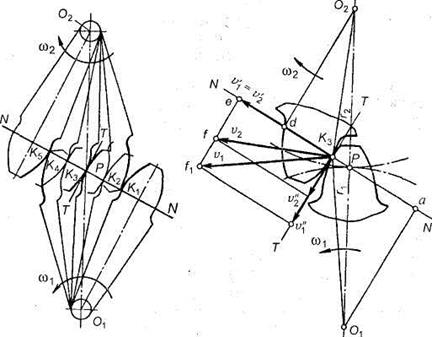
Основной закон зацепления профилей зубьев колес зубчатых передач гласит: для нормальной безотрывной работы передачи, составленной из двух профилей, входящих в высшую кинематическую пару, необходимо, чтобы нормаль к этим профилям в точке контакта в любой момент времени проходила через мгновенный центр их относительного вращения. Зубья зубчатых колес составляют высшую пару IV класса, то есть представляют собой некоторые поверхности, находящиеся в контакте. Таким образом, профили зубьев — это кривые а в некоторых случаях прямые линии. На рисунке 34 показаны два профиля, находящиеся в контакте в точке А. Скорость точки А, принадлежащей первому профилю V 1 , перпендикулярна радиусу О 1 А, соответственно, скорость точки А, принадлежащей второму профилю V 2 , перпендикулярна радиусу О 2 А. Рассмотрим проекции этих скоростей на общую нормаль N-N , проведенную к профилям в точке их контакта С 1 — проекция скорости V 1 , С 2 — проекция скорости V 2.

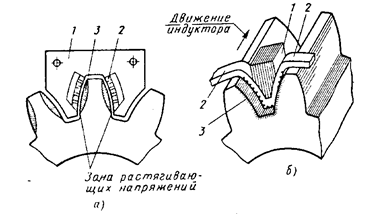
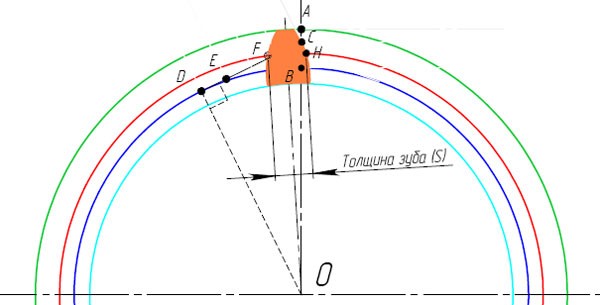
Боковой зазор получается за счет уменьшения толщины зуба. В стандартных зубчатых колесах толщина зуба одного колеса из пары определяется вычитанием половины общего бокового зазора из половины окружного шага. Когда требуется работа передачи без бокового зазора, основные размеры колеса должны выдерживаться в крайне жестких пределах.
- Обычно термины зубчатое колесо , зубчатка и шестерня , по мнению обывателей, являются синонимами, но некоторые авторы называют ведущее зубчатое колесо шестернёй , а ведомое — колесом [2]. Однако согласно ГОСТ шестерня — зубчатое колесо передачи с меньшим числом зубьев при одинаковом числе зубьев зубчатых колес передачи шестерней называется ведущее зубчатое колесо ; колесо — зубчатое колесо передачи с большим числом зубьев при одинаковом числе зубьев зубчатых колес передачи колесом называется ведомое зубчатое колесо.
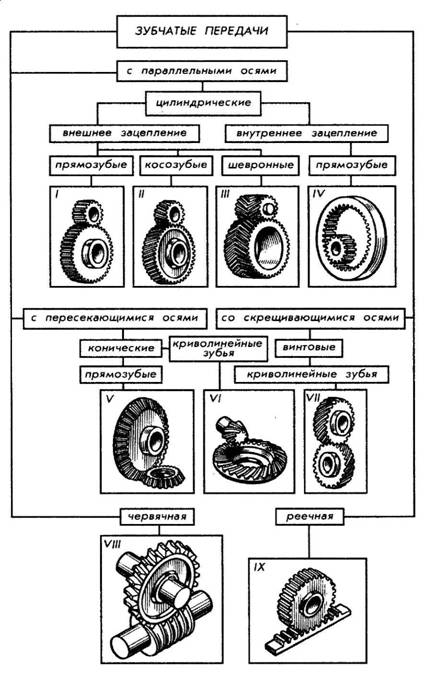
- Общие сведения и классификация зубчатых передач. Достоинства и недостатки зубчатых передач.
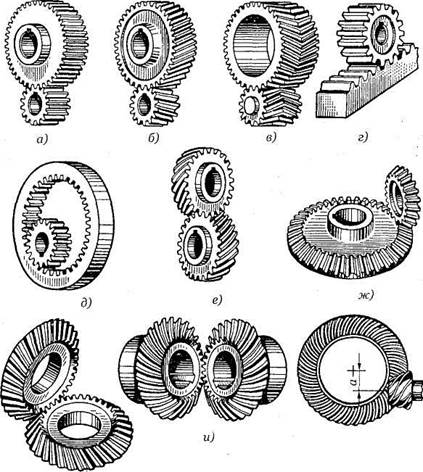
- Обычно, зубчатые колеса и шестерни выполнены в форме дисков с характерными, для них, нарезными зубьями. Прямозубые колеса применяются них окружных скоростях, большой твёрдости зубьев, в открытых и планетарных передачах.
- Определение основных параметров зубчатых колес с помощью инструментов. Цель работы : определение основных размеров зубчатых колес.
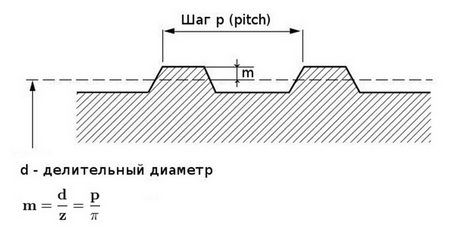
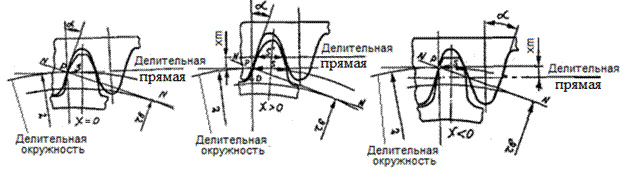
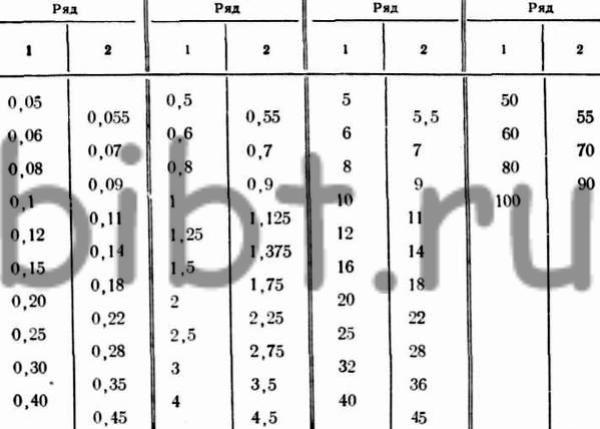
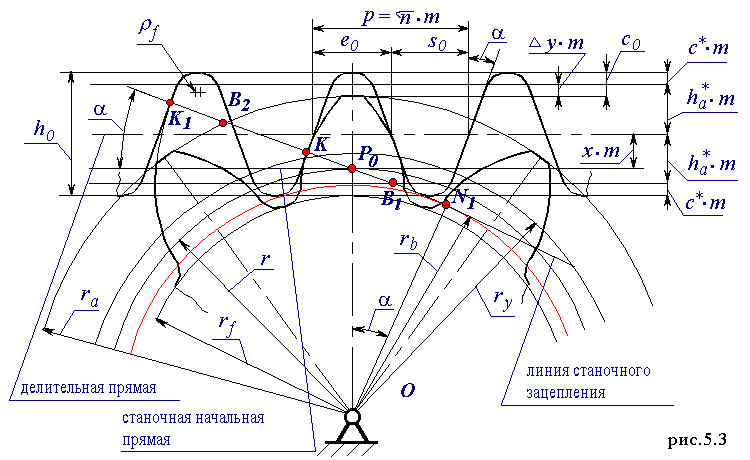
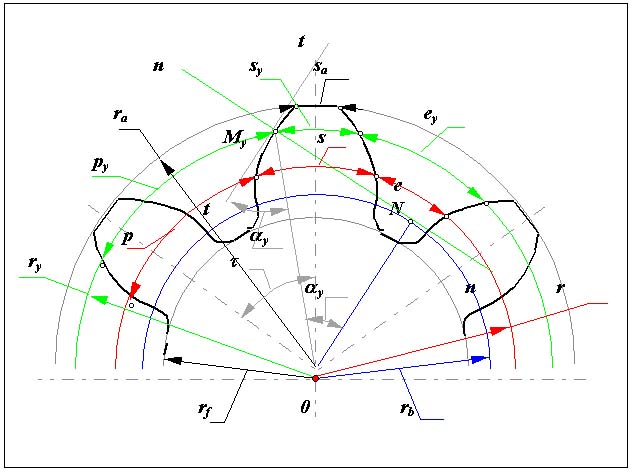
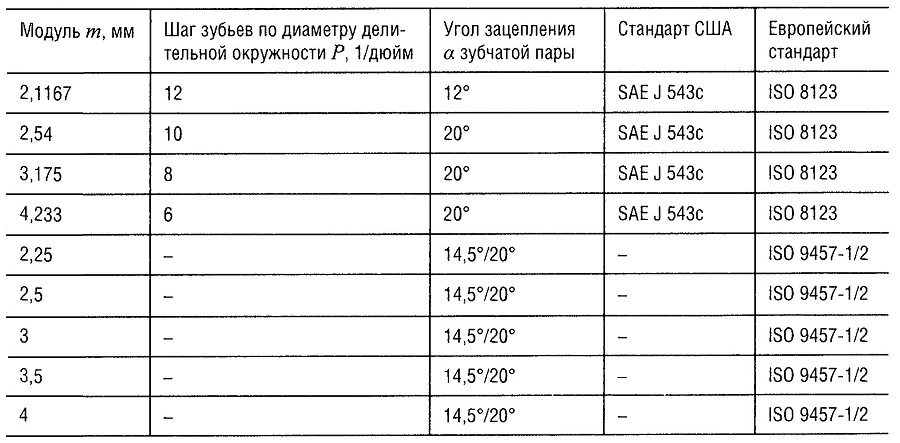
- Основной величиной, характеризующей размеры зубчатого колеса, является модуль, который обозначается буквой m. Соответственно различают модули: окружной m t , осевой m x , нормальный m n и др.
- Портал Проза. Все авторские права на произведения принадлежат авторам и охраняются законом.
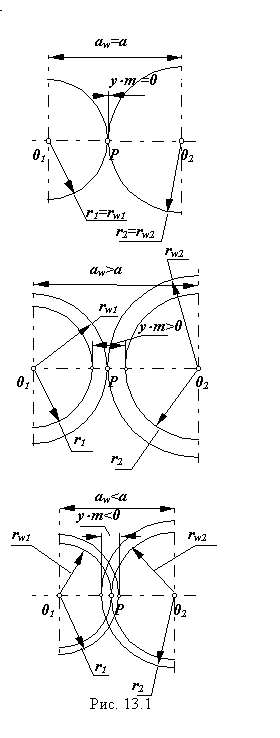
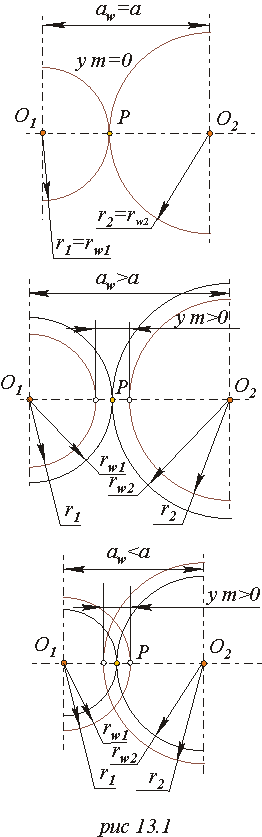
- Цилиндрические эвольвентные зубчатые передачи в зависимости от величины воспринимаемого смещения классифицируются следующим образом. При проектировании зубчатой передачи необходимо решить несколько задач:.
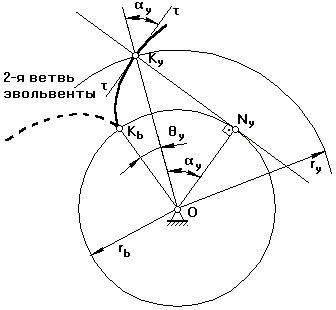
- Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей.
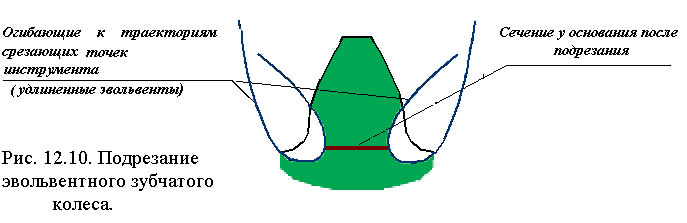
- Нарезание колес с эвольвентным профилем зуба в приборостроении производится методом обкатки при индивидуальном производстве колеса нарезаются методом деления.


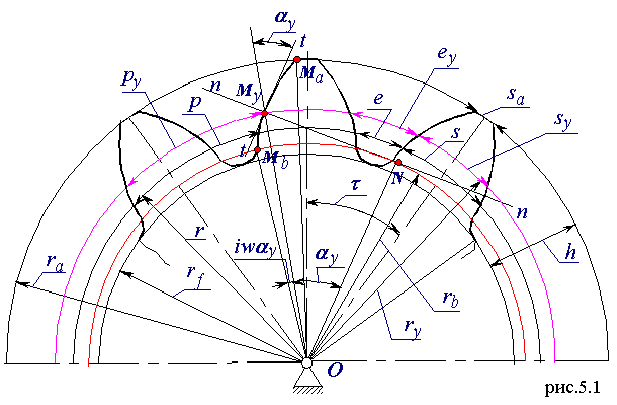

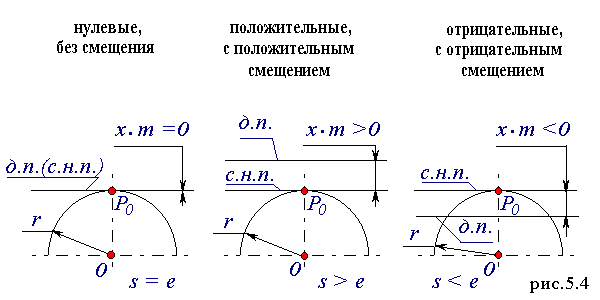

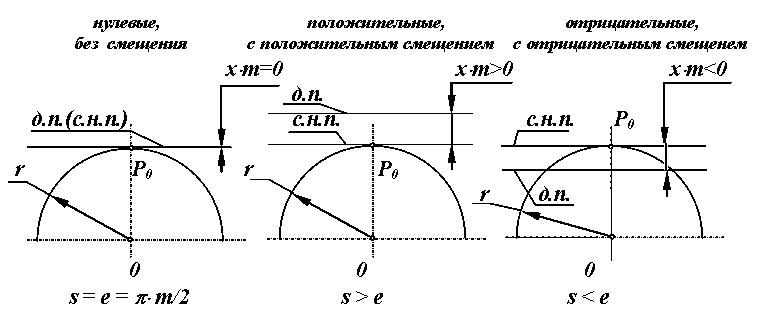

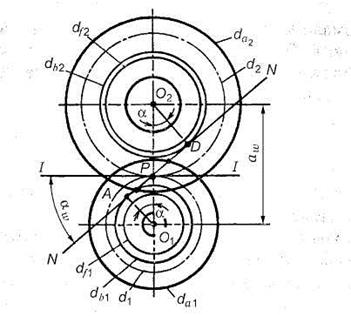

Лекция 8. Сопряженные поверхности — поверхности, которые постоянно или с определенной периодичностью входят в зацепление друг с другом. По отношению к начальным окружностям сопряженные поверхности могут занимать различные положения. Правильным положением является то, которое удовлетворяет основной теореме зацепления, теореме о мгновенном передаточном отношении, которое формулируется следующим образом:. Общая нормаль, проведенная в точке контакта сопряженных поверхностей, проходит через линию центров О 1 О 2 и делит эту линию на части, обратно пропорциональные отношению угловых скоростей.